推荐理由：空间观念是个体对空间、图形及其关系的直 觉，是一种对四周环境及对环境中物体形状的几何 观点。现实中，空间观念所启示的对象及结果有趣 且有重要价值，已经渗透到数学领域。随着计算机 技术的普及，几何语言成为日常生活中非常重要的 工具，也促进了空间观念在其他领域的广泛迁移。 事实上，空间观念的核心是空间想象，本质是形成 空间思维，想象和思维连接并直达创新与创造。因 此，相对传统意义上的数与代数、图形与几何，空间 观念的发展对义务教育阶段学生而言是更为迫切的需要。

一、“做数学”在学生空间观念发展中的作用

一线数学教育工作者往往认为：“学生空间观 念的差异是天生的，后天难以改变。”研究表明，如 果没有适当的训练，大多数人的空间观念是不会发 展的，只能停留在原始的层面上[1]。中小学生空间思 维的差异很大，比如用平面截正方体后所得截面的 形状，空间思维能力好的学生理所当然认为可以有 三角形、四边形、五边形和六边形；大部分学生会认 识到除了四边形，还可能有三角形；而空间思维能力较弱的学生无论如何只能想到四边形。 学生形成空间观念的困难在于：难以直接感知周围环境和实际物体，难以领悟二维图形与三维图 形及其相互关系，难以感悟图形变换及其性质。如 同不可能让学生在书本里学会游泳，在 PPT 里发现 理化生实验结果一样，发展学生空间观念不可能只 通过教师讲解和反复解题，更需要学生的动手操作 和亲身体验。正如弗赖登塔尔在论及空间思维的发 展时所说“把学生在物理空间的具体活动，通过抽 象、绘图、做出模型等有限步骤达到几何直觉的最 高阶段的道路清晰描绘出来，是有巨大的教育学方 面的好处的。”“做数学”是以“做”为支架的一种数学学习活动，学生运用材料和工具，在手脑协同的过程中，理 解数学知识，发现数学规律，创造性解决问题，发展 数学核心素养[2]。由此看来“做数学”于发展学生空 间观念而言并不是新鲜的学习方式，而是必然的学 习需求，只是“听中记”“题中熟”的学习方式泛滥， 淹没了应有之意的“做数学”。

二、做数学”发展学生空间观念的要求

空间观念由一系列通过构建与运用心像来表征空间物体、关系与变换的认识过程组成，学生空 间观念的发展需经过对他们所看到的图形形状及 特征的了解、抽象、概括、分析与综合的过程，因此， 只有在充分认识几何世界的基础上，学生的空间观 念才可能更为完备。空间观念的发展是一个思维进 阶的过程，表现为空间感知、空间表象、空间想象和 空间推理等认知水平的阶段性递进发展。不同认知阶段学生空间观念发展的任务和内 容载体不同“做数学”的任务、活动及必要工具也 不同（见表 1）。

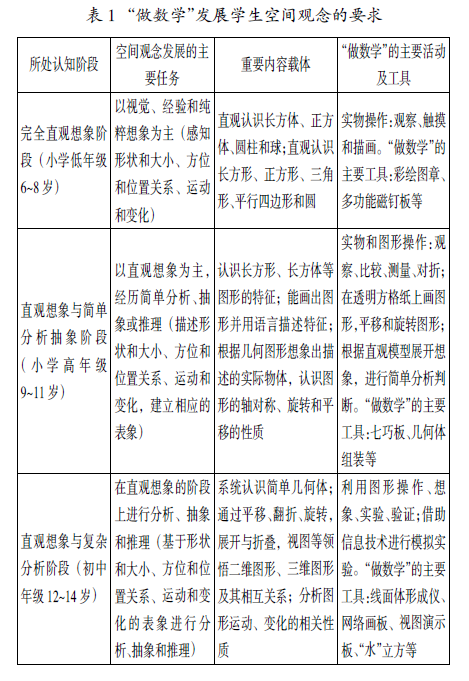
三、“做数学”促进学生空间思维进阶的 基本形态

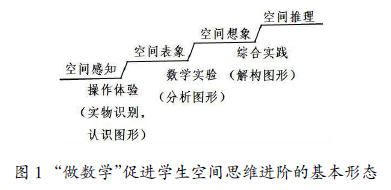
“做数学”通过操作体验、数学实验及综合实践 等形式，经过实物识别、认识图形、分析图形和解构 图形的过程，实现空间思维进阶（如图 1）。以学生空 间思维的阶段性表征为线索，阐述“做数学”在发展 学生空间思维中的实践内涵及价值效果。

1.援操作体验：操作实物，建立空间表象空间表象的基础是空间感知，即在大量空间知 觉的基础上，形成关于物体和图形的形状、大小及相互位置关系的印象。“儿童的智慧在指尖”，然而 数学对象及内容的高度抽象性，容易忽视小学低年 级学生的认知需要经历对实物的观察、触摸和描画 等直观感知阶段。忽视这一点，实际是忽视了学生 由具体到抽象的空间感知和图形抽象的过程，如此 学生图形识别等空间表象能力的发展就会受到制 约。比如正方体的主视图，学生实际认可的往往是  图 2，至于后期解决类似问题时又认为是正方形，多 是在习题的反复训练中记忆与模仿的结果。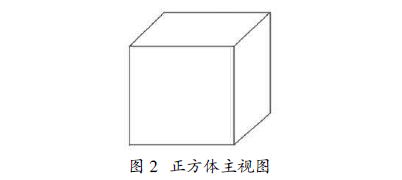

操作实际物体，可以让学生在“做”中真实而深 刻地认识图形、理解图形，真正意义上完整地经历 感知空间—抽象图形—建立空间表象的过程。案例 1.把平的面请到纸上 目标：经历空间图形转化为平面图形的过程。 实物：积木、印泥和钉子板等。 步骤：（1）印一印、描一描。用印或描的方法将积木的面请到纸上。（2）分一分。将印或描出来的图 形分类，并命名。（3）围一围。在钉子板上将印或描 出的图形用橡皮筋围出来。案例 2.“折出”正方形和长方形的特点

目标：通过实践操作，发现正方形和长方形的特点，同时积累数学活动经验。

实物：彩纸、直尺、三角板和钉子板等。

步骤：（1）折一折、量一量。通过折正方形、长方形，观察边和角的特点，再用直尺、三角板测量验证。（2）围一围。在钉子板上用橡皮筋围出正方形和长方形，通过移动橡皮筋将正方形和长方形分别变为长方形和正方形。（3）说一说。说出前两个活动中自己的发现、可能的理由。能不能用钉子板围一个圆？

操作体验促进空间思维发展的内涵：案例 1 用积木印出一些面，引导学生经历从立体到平面、从 具体到抽象的过程，以此认识基本的平面图形。在 这些具体的实验活动中学生领悟到周围环境中的 立体实物有不同的面，这些面通过描画在纸上，就 抽象为数学的研究对象。案例 2 用折一折、量一量、 围一围的实验探索长方形和正方形的特点，进一步 从性质特征的角度加深对图形的认识。同时也积累 数学活动经验，即以后再研究其他图形特征时可以 通过类似的方式研究图形的边、角关系。

认识图形是一个感知、抽象的过程，不仅是让 学生区别图形和名称概念，更重要的是通过认识图 形学会根据图形特点进行分类。学生容易区分差异 大的图形，比如三角形和四边形；差异较小的图形 区分就有困难，比如长方形和正方形。正方形是长 方形的特例，仅仅记住定义是不行的，必须动手操 作，在操作的过程中从本质上认识图形的特征，积 累包括思维层面、实践层面的数学活动经验。这些 特征往往是图形间对比的结果，这种对比是分类标 准建立的过程，比如钉子板能围出圆吗？2.数学实验：实验思考，发展空间想象心理学把人对头脑中已有表象进行改造，创造 出新形象的过程称作想象。没有想象，很难谈到对 现实世界的了解与把握，很难谈到发明与创造，因 此发展学生的空间观念一定要重视想象。空间想象 就是以现实世界为背景，对头脑中已有的几何表象 进行加工改造，创造新形象的过程。空间想象是建 立空间观念的核心，它表征为建立并操纵二维和三 维物体的心智，从不同角度观察物体的能力，既包 括从现实物体到平面图形的抽象，也包括从平面图 形到现实物体的想象。案例 3 .从不同方向观察物体实验目标：经历不同方向观察物体的过程，把 三维空间的图形转化为二维图形；由平面图形想象 空间图形，实现二维向三维的转化。实验工具：正方体、圆柱体、长方体、圆锥、三棱 锥、四棱锥等积木若干，正方形塑料片若干，橡皮泥 若干。实验步骤：（1）摆一摆，画一画。用 4 个正方体 积木搭出“L”形，再从这个物体的前面、右面和上面 观察，借助摆正方形塑料片或者在方格纸上画图等 方式，将每次看到的“样子”摆或画出来。（2）反方向 摆一摆，画一画。用这 4 个正方体积木搭出反“L”形 物体，同样从三个面观察，用正方形塑料片摆或在 方格纸上画看到图形的“样子”。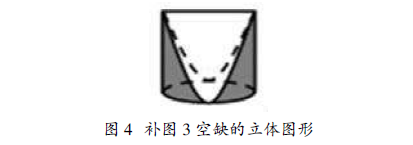（3）议一议，摆一摆。给定一个方向观察到的形状，摆出可能的物体； 给定两个方向观察到的形状，摆出可能的物体；给 定三个方向观察到的形状，摆出可能的物体。（4）想 一想，堵一堵。选择积木堵一堵图 3 中的正方形、圆 和三角形，如果只堵其中一种，你有什么发现？如果 只堵其中两种呢？将三种都堵上呢？如果没有你所 需要的积木，请用橡皮泥设计一个你认为可以的立 体图形。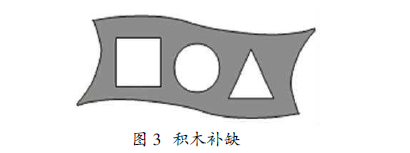

数学实验促进空间思维发展的内涵是用同样 的小立方体拼搭成组合体，从组合体的前面、右边 和上面观察，想象观察的图形，这是形成空间想象 力的基础。这个实验的关键，首先是观察方法的规 范；其次是用正方形拼出看到的图形，在方格中画 出看到的图形，实现“思维的可视”，促进学生的想 象；最后是通过比较，引导学生感悟对于不同的物 体观察到的面的形状相同或不同。步骤（3）是给出 从某个方向看应该看到的样子，让学生用 4 个小正 方体积木搭出符合特征的物体，交流汇总，学生能 搭出多种不同的物体，但从每个方向看到形状都相 同；增加一个方向看到的形状，符合的搭法少了；再 增加一个方向看到的形状，符合的搭法只有 1 种。 步骤（4）是进一步由二维到三维的空间想象，尤其 是设计出同时能堵住正方形、圆和正三角形的立体 图形，具有较大的挑战性，学生必须在前面三步实 验操作形成空间图形表象的基础上，产生新的表 象，同时感悟到从三个面看能够唯一确定立体图 形。设计出或者认识到如图 4 的立体图形表明学生 已经建立了较好的想象力。

空间想象是对头脑中已有空间表象进一步抽 象的存在，也就是说它不是看到过的具体物体的复 制，而是头脑中存在的抽象了的图形，正如郑板桥 所谓“其实胸中之竹，并不是眼中之竹也”。对已有 空间表象的加工、改造和结合往往有一个顿悟和豁 然开朗的过程，这个过程就是空间想象建立的过程，数学实验可以促进这种想象力的产生。3.综合实践：实践探究，形成空间推理推理是数学的基本思维方式，也是生活生产中最常用的思维方式，空间推理是在对空间图形进行 结构分解基础上，对结论的有逻辑的判断、验证和 分析，它不仅表现为结论的获得，还表现为新问题 的发现和提出。数学实验有助于空间推理能力的发 展和新问题的发现与创造。案例 4.探究正方体截面的形状综合实践目标：通过“水”立方探索正方体截面 的形状，发展空间推理能力和发现问题、提出问题 的能力。综合实践任务：探究正方体截面的形状。生活 中很多富有美感的物体都是基本图形的组合，比如 造型各异的钻石就是原石经切割、打磨而成的。制 作前的设计需要有很好的想象力，比如一个正方体 沿平面切一刀，截面会是什么形状？综合实践活动：如果不能准确的想象出结果， 可以做具体的实践活动，比如设计替代物进行实践 探究。综合实践工具：两类含水量不同的“水”立方若 干个。综合实践步骤：（1） 猜想：用一个平面截正方 体，所得截面形状有哪些？能否设计工具在“做”中 发现结论？（2）操作“水”立方，观察水面会有哪些形 状，与你的猜想是否一致，据此你能提出哪些新的 猜想？能说明你的猜想的合理性吗？（3）观察水面呈 现的四边形的特点，并说明理由。（4）类比四边形， 说说五边形、六边形截面的几何特征。（5）操作水立 方，还有其他发现吗？综合实践促进空间思维发展的内涵是：正方体 截面的形状是一个空间思维要求比较高的问题，仅 仅凭借抽象的思考，学生很难想通，更难以发现截 面形状深层次的结构特征。“水”立方数学实验工具 把水面当成正方体的截面，通过调节“水”立方的摆 放方式，可以直观观察正方体截面的形状。同时，学 生会发现，水面和正方体的每个面相交都形成了截面的一条边，正方体有六个面，所以截面最多是六 边形。步骤（3）是对具体截面几何特征的深入观察： 截面四边形可以是正方形、平行四边形、菱形、梯 形、等腰梯形，好像都至少有一组对边互相平行，进 而推理出正方体任意 4 个面中至少有两个面是相 对的，它们互相平行，观察发现和它们相交的截面 也是平行的。进一步推理：截面是五边形时，5 个面 里至少有 2 组面是相对面，所以五边形截面有两组 边互相平行。步骤（5）引导学生进一步发现，水量少 的“水”立方呈现不出六边形水面，水量多的“水”立 方呈现不出三边形水面，那么，形成六 边形（三角 形）的最少（最多）水量分别是多少呢？如果正方体 的截面图形是三角形，切割后的立体图形会是怎样 的？四边形、五边形、六边形呢？直观想象能力是空间思维的核心，学生的空间 思维往往表现为“理所当然如此”，也常处于“知其 然不知其所以然”的状态，“做数学”不仅让学生发 现结论，而且通过空间推理认识结论的合理性不是 偶然而是必然，同时进一步发现新结论，并深入推 理论证。实物识别、图形认识、图形分析和图形解构等 空间认知水平在同一个体中有时是交错共存的，即 同一学生在某种场合下表现出此种水平，而在另一 情境中又可能表现出其他水平。因此“做数学”促 进学生空间思维进阶，并不是严格意义上的阶段划 分，而是一般状态下，学生空间思维发展的阶段描 述，目的是藉由“做数学”更清晰地认识空间思维发 展的意义、认知状态和形成过程。