推荐理由：章勤琼博士在数学文化领域有着深入的研究，他分享的案例有一定的理论深度，还独具趣味性。《数学中的“直观”》与工作室研究的“数学与传统文化”“数学与学科融合”两个方向有较大关联，起到了理论引领的作用。

 核心素养为中小学老师和研究者们提供了大方向，而核心素养的最终实现是需要落实到各学科的具体教学中的。数学核心素养提的三句话特别好：用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界。分别对应数学的三个基本特征：概括性、严谨性和应用的广泛性。其中数学的思维思考现实世界最突出的是推理，这体现了数学严谨的思维方式。但是，数学除了严谨的推理之外，其实还有一种非常重要的思维方式，那就是直观想象。数学中有很多结果其实都是直观地“想”出来，甚至是“看”出来的，而不是一步一步推导出来的。如果数学家没有了直观想象的灵感，相信人类的数学绝不是现在这个水平。尤其是在中小学阶段的数学教学中，更需要凸显数学的直观。

一、几何直观
几何直观是义务教育阶段提出的十个核心概念之一，笔者曾经跟史宁中有过面谈，问及小学阶段跟高中阶段的数学核心素养上是否有所不同，他说，总体来说应当是一致的，只是存在一些具体内容上的差异。比如说，直观想象应该包含几何直观、代数直观和统计直观，但在小学教学阶段应以几何直观为主。代数直观和统计直观对小学生来说都太难了。
在《义务教育数学课程标准（2011年版）》中指出：”几何直观是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。“请注意这里的关键词，几何直观是指利用图形描述和分析问题，而这里需要描述和分析的问题往往不是几何的。美国著名的数学科普家马丁加德纳在1973年10月发行的《数学游戏》专栏中专门讨论过”无需语言的证明“（Proof Without Words，简称PWWs)，指出“在很多情况下，沉闷的证明可以辅以几何模拟，而且这是如此简单、美丽以至于瞬间就可以看到定理的真相。”而到了20世纪80年代，美国数学协会出版的杂志，如《数学杂志》，曾经专门征集过PWWs的例子。其中出现了很多绝妙的例子。譬如大家最熟悉的等差数列的求和。

这个图形一看就能理解等差数列是如何求和的，事实上，可以帮助你理解这个的还不止这一张图，比如：

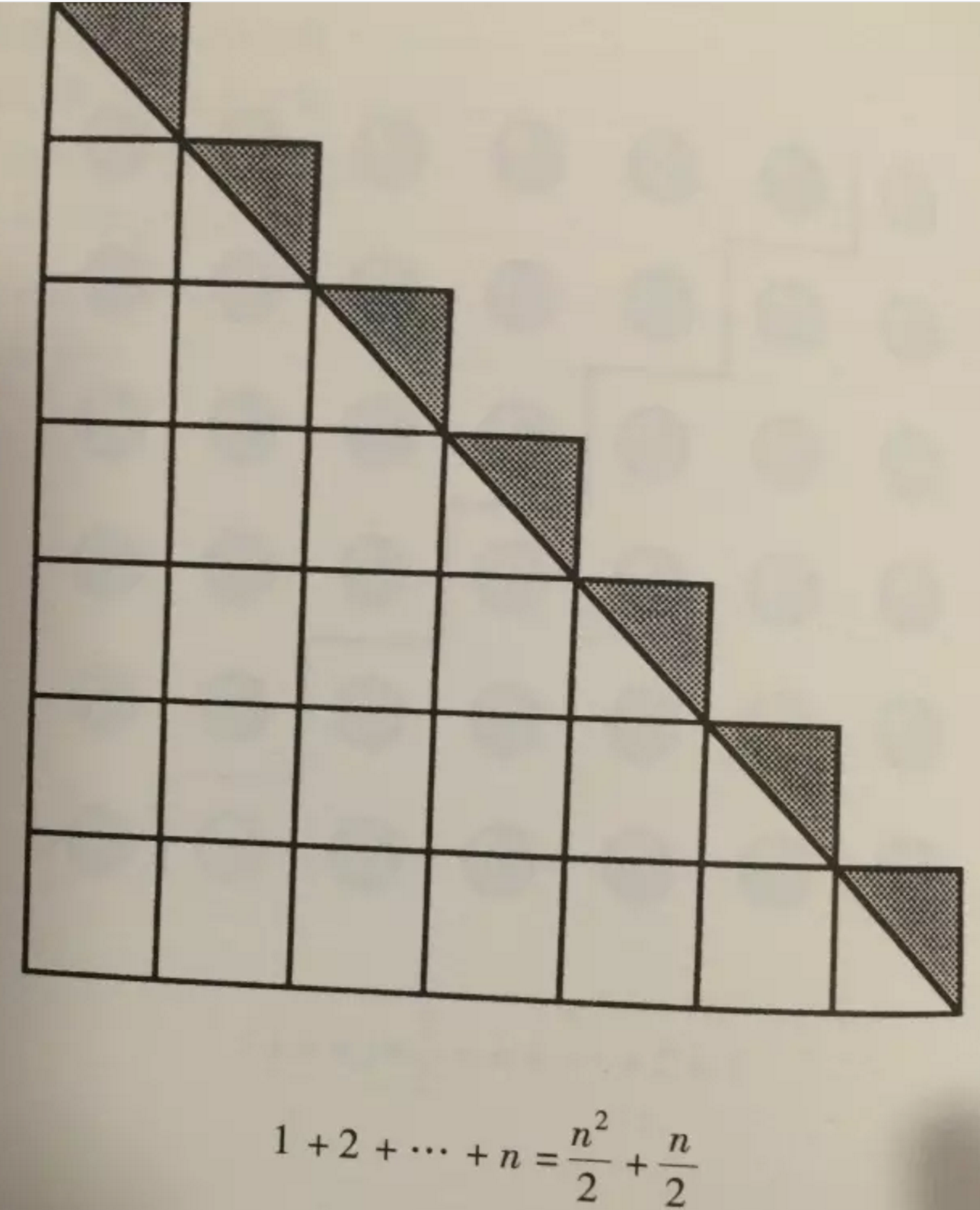
当然，几何直观能说明的问题还有更复杂的，比如：


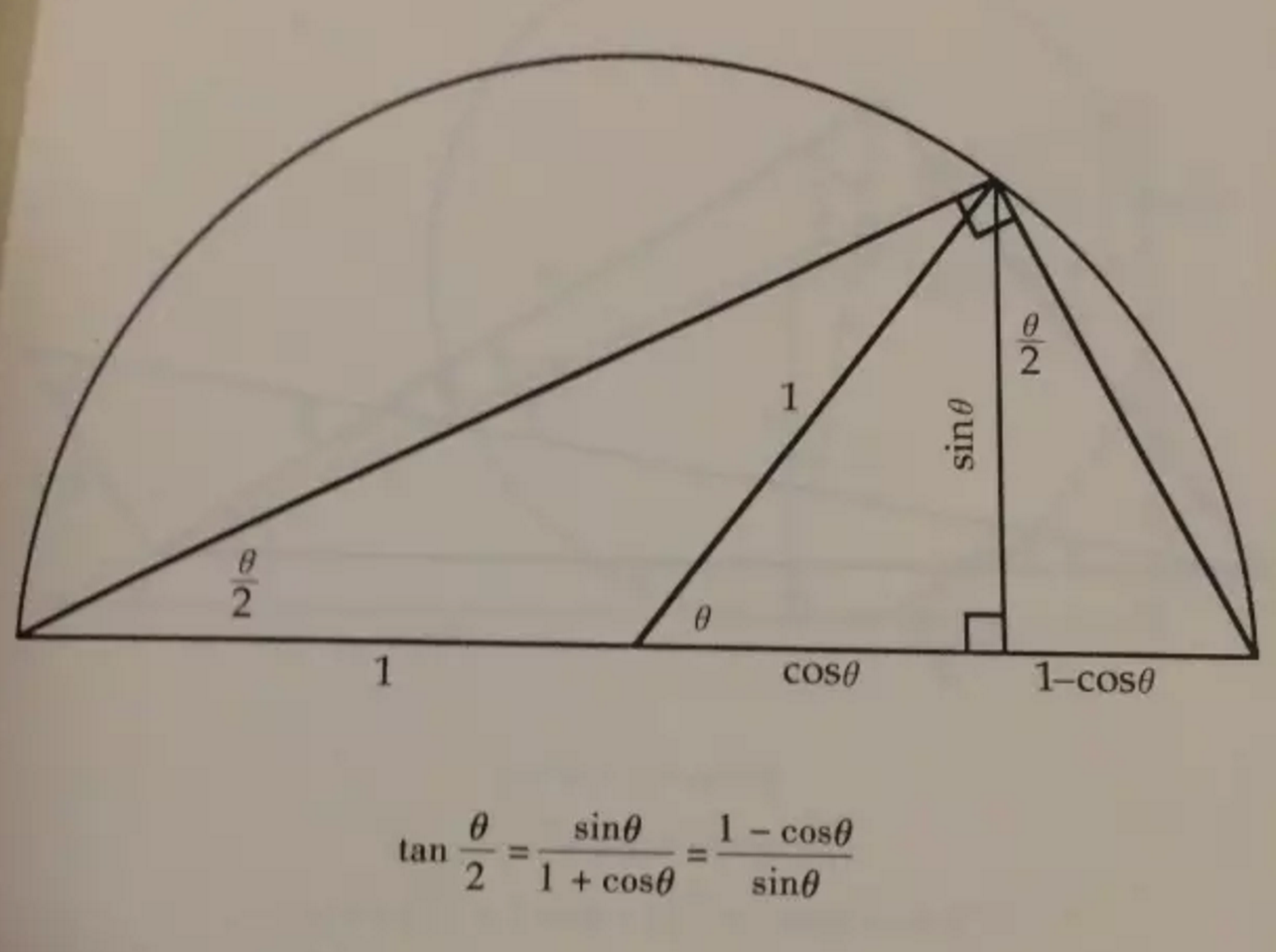
再举一个2002年在北京召开的国际数学家大会的Logo，这个图来源于赵爽弦图，是证明勾股定理的一个重要代表方法之一。

事实上，关于勾股定理的说明，更有趣的当然是下面这个动图。

而2016年德国汉堡召开的ICME13的会标则是对上述勾股定理基本图形的变形，易见，从直角三角形上长出来的三个图形虽然由曲线构成，但面积和的关系仍然存在。
二、生活直观
事实上，除了几何直观之外，还有其他模式的直观，比如下面这个例子。如果让你写出一个介于7/8和8/9之间的分数，要求分母最小，你会怎么写？首先想到的当然是通分，两个分数分别通分后得到63/72和64/72，还要再将分子分母各乘以2，得到126/144和128/144，然后写出的分数是127/144。这个过程当然没有问题，但容易知道144肯定不是最小的分母。有很多方法能写出符合要求且分母比144小的分数。但，这个时候，如果有个学生写了一个数15/17，显然，他将分子和分母分别相加了。首先，请问这个分数是否是满足条件的，即介于7/8和8/9之间呢？经过计算，的确是符合条件的。接下来一个问题要更复杂些，给出两个真分数a/b和c/d，其中a/b<c/d，是否总可以拿分子分母相加的方法得到介于两个数之间的分数呢？也即，a/b<(a+c)/(b+d)<c/d是否总能成立？你会发现，要说明这个并不容易。
那么，我们先讲这样一个生活中常见的事情，给你两杯糖水，其中第一杯糖水为b克，糖为a克；第二杯糖水为d克，糖为c克。假设第一杯糖水的浓度要低于第二杯，现在将两杯糖水混在一起，那么混合后的糖水浓度就是(a+c)/(b+d)。两杯不同浓度的糖水混合以后，浓度显然要比原先淡的那杯浓，而比原先浓的那杯淡。这可不就是刚才的不等式？
那么，根据这个糖水浓度实验，你还能给出怎样的分数不等式呢？对了，就是a/b<(a+c)/(b+c)。在一杯糖水质量为b克，糖的质量为a克的糖水中加入c克糖之后，显然会变得更甜。
再来看另外一个例子，

其中证法二是不是更直观？更有操作性？更有趣？
三、有关直观的另一个有趣的例子
再看这样一个题目，这个题目是我读师范时的一个同学，现在在温州建设小学教数学的池捷老师在微信圈里出的题目，他的数学功底超乎一般的小学数学老师许多。请诸位为乌有国王出个主意：500桶酒，其中1桶是毒酒；48小时后要举行酒会；毒酒喝下去会在之后的第23-24个小时内毒死人（也就是喝了毒酒能活23小时，活不过24小时）；国王决定用囚犯来试酒，不介意囚犯死多少（呃，我想说这种暴君一定不是我大中华民族的），只要求用最少的囚犯来测试出哪一桶是毒酒，问最少需要多少囚犯才能保证找出毒酒？我一看到这个题目时，想当然地把这个题目想成了将500化为二进制数，然后有9位数字，最多只需要8个1，所以需要8个囚犯，分别充当二进制数中的1就可以。而由于是48小时，所以可以进行两次，在第一次中先把数字中含1少的数字先试，如果没有，则先排除一半，然后再进行第二次，这样应该还是需要4人。
但后来，看到答案之后觉得简直太巧妙了：两人就够了，把酒排成23×22的方阵，第1个囚犯每小时喝1列，第二个囚犯每小时喝1行，由于毒发的时间是精确到小时数的。所以根据两人的毒发时间可以分别精确到具体的行和列，这样就能找到毒酒所在的坐标。这个解法是不是很直观？一个看似跟几何毫无关联的题目，就这样用几何的方法解决了。更有趣的是，这个题目如果改成10000瓶毒酒更有趣，因为如果引入空间坐标系，只需要三个囚犯就足够了。1个囚犯，最多只能找出23瓶酒中的毒酒；2个囚犯，就是529瓶；3个囚犯，则是12167瓶！这种几何级的增长是不是让人叹为观止？更进一步，n维向量是不是也可以由此引入？
此外，还有一个有趣的事情。利用向量确定坐标的方法，是2个人必死。而如果用二进制的方法，则有可能只要死1个人。那么到底应该用哪种方法更好？这里其实已经涉及到统计直观的问题了。用二进制的方法，只死1个人的可能情况只有9种，此外还有死2人、3人、4人、5人的情况，按照期望来直观判断，肯定是要多于2人的。所以，还是要选择向量的方法。
四、在教学中还可以怎样利用直观？
直观应当是小学生认识世界和数学的首选方法，尤其是对几何图形的认识。那么在图形的认识的教学中是否可以利用这一点呢？我想应当是可以的。
比如，在对三角形的认识的教学中，三角形的分类是一个重要内容，分类可以按边分，也可以按角分。那么到底应该是按边分进入还是按角分进入呢？不同的老师有不同的选择。那么我们是不是可以把选择权交给学生的直观认知呢？比如给出一堆不同形状的三角形，其中有等边三角形和直角三角形这两个最特殊的三角形。交由学生来根据直观选择他们认为最特别的三角形，看到底是等边三角形还是直角三角形给学生的刺激更强。如果学生更容易看到的是等边三角形，那就由边进入；如果更容易看到的是直角三角形，那就由角进入。
另外还有需要说明的是，一般老师们在教学的时候，如果按照角分类，都是直接就给出锐角、直角、钝角三类三角形。但按照史宁中《基本概念与运算法则》中的说法，学生在没有任何理论基础的情况下，要直观体认到锐角三角形和钝角三角形的区别是非常困难的。“在分辨锐角三角形和钝角三角形的过程中有一个重要的分水岭，那就是直角三角形。事实上，在分类的过程中，制定标准的核心就是找到分水岭。因此在教学中，可以给出下图，其中的直角三角形就是分水岭，在借助下图分辨锐角三角形和钝角三角形的过程中，让学生感悟分水岭的作用，为学生学会自己建立分类标准提供几何直观。”

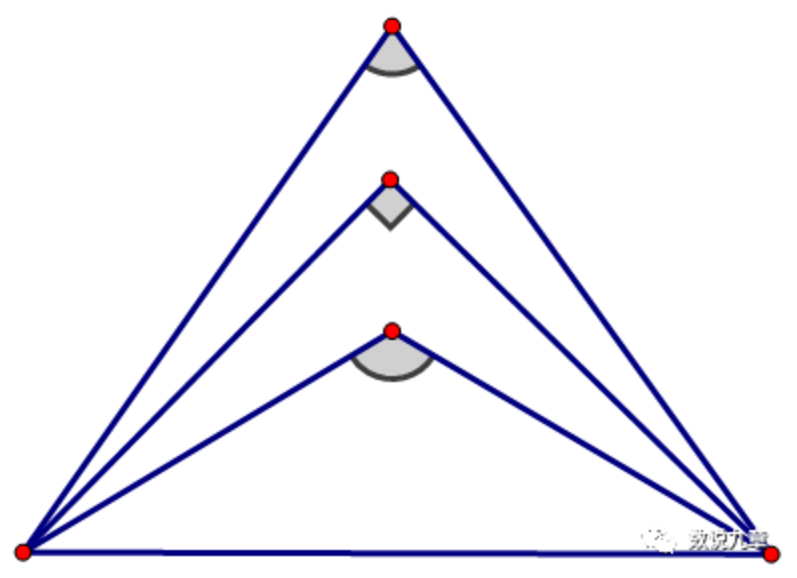
因此，在三角形的分类的教学中，在按角分类这里，是否可以首先由学生的直观体认来给出直角三角形和非直角三角形的区别。再进一步将非直角三角形分为锐角三角形和钝角三角形呢？

附件：