——评苏科版七年级下《证明（1）》

周建香（江阴市敔山湾实验学校）

 

 

本次课型研究听、评课内容为苏科版七年级下《证明（1）》。从课型分类视角，属于新授课型，课堂教学的设计、展开应尽可能围绕新授课的特征，彰显新授课的教学艺术，梳理新授课的教学要点，挖掘新授课的核心价值，开辟新授课的授课新视角。

一、教材研究：析透本质

分析教材，研究教材，析透其思想本质，方能理解教材，应用教材，开发教材，拓展教材，最终高于教材。

析：教者的原本分析：“在学生经历了将近两学期的初中数学学习中，经历过观察、实验、操作、猜想、类比、归纳等数学活动探索了一些图形的性质，一些数学结论，感受到了以上数学活动得到的结论基本都是正确的，积累了不少的直观判断经验。但仅仅凭借观察、实验、操作是不够的，有时甚至是错误的，这就是这节课学习“证明”的必要性与迫切性。”

再析：针对教者的分析可以看出，教材分析缺失，学生分析略浅，点面化分析较少。其实，学力基础远远不止初中二年积累，应追溯至孩子有动手、思维的自觉意识，至少也是进入校园生活起始。大量的生活实例，学习范例已经储存，只不过未曾给予“证明”的正式“命名”。而学情背后还有“案情”。案例本身就有着悠久历史，各种理论、实践的支撑不胜枚举。不妨举之例之，更有似曾相识之感，更有激发性、“诱惑力”。分析空洞。即使是分析学生，也需点面结合。将本课的使命融入本章节、本册书、整套教材，站得高一点，看得远一点，立意深一点，课型明确些，设计精准些。

透：所谓透即是对本课要表达的数学使命理解通透。为什么要在这个章节安排这节课？《证明（1）》意欲何为？想传达给学生什么信息？怎么传达？传达到什么层次？课上要达到什么预期效果？每个教学点该如何设置？有无细化目标？预设怎样？…通过层层的设疑，教者逐步理清教材的编排意图，吃透教材。通透理解的条件下，精彩适切的教学设计、实践才有可能合理展开、生成。

本：这里的本有三个理解。一是案例这个“本”，二是学生这个“本”，三是教师这个“本”。

案例“本”：建议以本为本，挖掘拓展。学生“本”：以生为本，看清学生已有本事和要学本领，析出差异，弄清何处链接，以做到无缝对接。教师“本”：教师的本分是什么？是“教”。教师的本事是什么？是会教。教师教什么？是教本质。从“本”的层面看，教材不透，一课难成，一书难教。

质：质有两解，一者，问题的本质，即本课的核心。还是得从教材入手，研教材，钻课标，获得一节课的核心任务，核心知识，核心主线，核心问题。二者，质量、效率。就本课而言，核心是感受证明的必要性，忆曾经的证明种种，看今朝的证明翩翩，为今后的证明、推理开萌、引路。

综上，教者对于12.2《证明（1）》的教材分析、研读有一定收获，但核心、本源性理解有所缺失，建议在教材研究、课标把握方面做一些总结、提升。毕竟，只有析透教材，明确意图，才能制定出鲜活的三维目标并落实于教学实践，切实把控课堂教学的各个环节，以生为本的为课堂教学服务。

二、教学视点：明确主线

教者课堂实践表现的主题需更清晰，主线更明确，欲表达的思想、内涵力争透过课堂观察可发现。让原生课堂变得可测。

教者设计：

情景引入：在黑板上展示如图所示的两张弧形纸片

（1）纸片A、B哪个比较长？

（2）你用什么方法来检验你的判断是否正确？

 

 

 

观察思考：

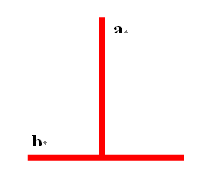
活动1：我们知道实验、观察、操作是人们认识事物的重要手段．线段a与线段b哪条比较长？说说你的做法。

a

b

 

 

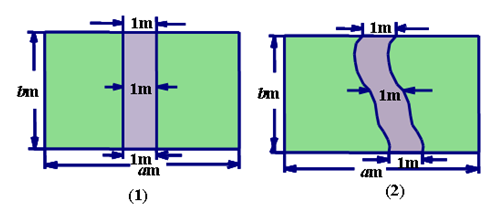
活动2：图（1）的长方形草坪中间有一笔直的小路，为了达到“曲径通幽”的效果，现计划修改为图（2）中的弯曲小路，这两条小路的面积相等吗？说说你的理由。

 

活动3：小明想研究代数式x² －2x＋2的值，于是他取了一些数值代入计算，得到了结论。

请你再取一些x的值代入代数式算一算，你能发现这个代数式的值有什么特征？并说说你的看法。

思考：本题中，你用什么方法去说明别人的观点不正确？你又是怎么说明自己的观点是正确的？

实验操作：

活动4：（1）图①拼成8×8的正方形纸片，把它剪成4块，两个直角三角形和两个直角梯形.

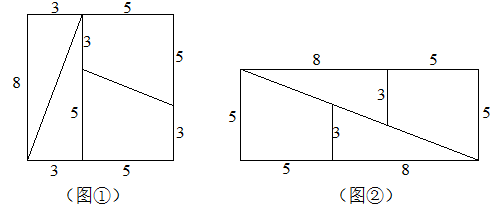
（2）这4块纸片按图②的方法重新拼合，能恰好拼成长为13，宽为5的长方形吗？为什么？

 

 

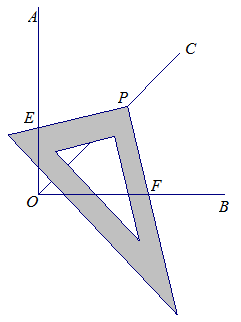
活动5：如图：（1）画∠AOB＝90°，并画∠AOB的角平分线OC。

（2）将三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边与∠AOB的两边分别交于点E、F，并比较PE、PF的长度。

（3）把三角尺绕点P旋转，比较PE与PF的长度。

你能得到什么结论？你的结论一定成立吗？与同学交流。

 

 

排除上课的实际情况，这里的环节设置较完整，问题类型很全面，除了素材1（情境引入）外素材本身没有问题。那么，利用这些素材可以做什么？借助素材有什么意图？每个素材怎样最大化展现本课核心“证明的必要性”？这些素材之间有无一个显性或隐性的主线，随着课堂的展开，主线逐渐清晰，学生的学就紧紧围绕这个主线，朝着中心“证明必要性”一路感受、体验、回顾、展望？注意切不可将本课理解或诠释成“技巧课”、“规律课”。

对于《证明（1）》，全课围绕的教学主线应是各种途径展现、体会证明的必要性。本课实质上不是证明的全新开始，早在七年级的各章节中都安排了各种形式的“证明”，本课的安排是给予揭示证明的时机，回顾教材、所学可见一斑。所以体会、感受证明，领悟其现实存在，承认其必要性是本课的中心主线，应将其细化并贯彻于课堂教学实践。

教者可设计连环情境，引导学生逐步感受、接纳“证明”这一新鲜事物。并预期学生能拾起这一新的武器武装自己的知识架构，改善解题策略，丰富数学思维，学会“以理服人”，“以证导学”。扩大学生数学问题解决的视野，增加“见识”，学会“分析”，提升数学素养。

建议教者设计活动以：“初步感受→进一步感受→对比感受→提炼感受→应用感受”为主线，沟通给学生的是一种情结，一种视角。即用“证明”的眼光看待周围的事物，学会“辩证”，既不盲从，也不全盘否定，用“证明”为自己开辟观察世界的新“视维”。

三、课堂实践：捕捉生成

生成是一节数学课最宝贵的意外财富。本课的主要生成点在活动3、4、5。活动3：不可能所有同学都是一致性的发现了结论“值总是正数”、“值不小于1”。采用小组讨论的方式直接扼杀了同学的个性化发现，小组内的结论往往都是盲从于个别平时有影响力的同学，其余“金光闪闪”的宝贵生成被简单“格式化”，被野蛮的“统一”。课上其实还有特别多的同学没有发现，也有部分同学有“惊人的发现”，诸如“得出的 代数式值总不小于代入的x的值”等。

活动4：能不能拼的问题其实很好判断，教者的教学顺序不符合学生的思维水平。不应该是先操作拼图、验证结论，之后再忽然发现计算很简单就能验证。其实，对于七年级的孩子而言，这本是个小的不能再小的问题。最要不得的就是问题还没解决，就先给学生一个下马威：这个是很难解决的，很高大上的。这种“教学恐吓”会切断学生的思维链条，被逼无奈走教师预期设定的解决路线。实质上，学生应该先独立思考是否可行？先发现的方法应是面积验证，而不是拼图验证，因为问题表述中已经给出了一张“是非图”。随着计算说理的浮出水面，拼图操作验证才有必要“眼见为实”。最终两种方式比较，感受其不同的证明风格，从“数”和“形”两个角度理解、探究，加深学生对证明的认识，深化概念。

活动5：教材提供素材的本意是什么？一定要按照素材本身，将几个问题都抛给学生吗？其实，活动5是活动1、2、3、4的生命力的延续。通过前面的活动，学生对计算说理、逻辑推理的感知渐深，活动5就是考察学生的证明思维是否已经建立。至于通过什么样的方式、具体怎样证明都不是活动5的核心。活动5的核心是“意识的激发，思维的引领”。所以，活动中应关注学生是否有“意识思维”的生成，及时捕捉、定格，将证明的意义引向深处，为后续证明的学习搭台。

四、教学把控：彰显智慧

适当的教学控制是有必要的。但把控的目的是防止偏离课堂中心，或节外生枝。岂不知，很多节外生枝都可以被教师引导为精彩生成，既展现数学魅力，又彰显教学智慧。不要害怕同学的意见多，很难统一，讲不清楚，导致课堂节奏变慢，预设内容无法完成等。

如活动3。为了能尽快完成活动，教师采取的是封闭管理。分组讨论就是封闭。数学并不是组内讨论就可以将个性全部显现，最终综合回答。相反的，组内只会存有一种强势学生的答案做主流，这无疑是把控过度。好的学生资源被埋没，好的生成资源被浪费。学生的智慧无法展示，教师的智慧更无法传递。

课堂上有出乎意料的情形并不可怕，将教学事故变教学故事，畅谈“算理”，力推“证明”。用应对教学意外的智慧疏导引流，变僵局为智慧场、生成源，提升学力更提升教品。

五、几点反思

反思1

就课堂观察看，全课教师、学生的行为表现平淡、无味，顺利、无奇。但就本课教材的安排而言，本课应属于“小鲜肉”型新鲜大餐，既有已经消化、吸收的前部大量“事实”做铺垫，又有棘手难解的新问题需探究，学生的思维应是活跃的，学生的情绪应是高涨的，学生的表现应是多样的，学生的意外应是不可避免的。那是什么扼杀了这些该有的“意外”、“生成”、“精彩”、“真实”？

1、学生被提前“告知”

学生被提前“告知”往往导致课堂反映平淡，教学贯彻“顺利”无碍，学生“猎奇”心理缺失。很多情况下，教师一些不严密的说辞，一些教学前置的行为会给学生新课的学习带来困扰。

如果在这一节12.2《证明（1）》之前，教师就曾经给予过数学证明的种种说明，那么，这一节新授课就变得没有新意可言。这节新课就如同鸡肋，无味且无奈。

2、教师的学情“失判”

教者对学情的失判会导致无法从整体上把握一节新授课。学生的基础究竟为何？认知有何障碍？能力有何不足？已学与要学之间究竟关键点在哪里？

就如同小学生学习26个英文字母，大量的拼音事实和学力基础已经建立，只是多一层含义，高一层理解。如何将英文字母教出新意？现在的问题是证明其实由来已久，教科书上证据不菲。如何既承认我们已经涉猎了大量的证明，方法从数和形两个角度都有，又要将证明当成一节新课来上？其实数学学习都是需要一定认知基础的，本课也不例外。完全可以由知识生长性视角展开教学，在回顾中感受，在新例子中感知，在新问题中感悟。

3、教学的死板“桎梏”

由于课堂教学是鲜活的，任何想用自己预设走完全课的流程式课堂教学实践终究是死板、桎梏的。

拘泥于课前预设，即使学情有所改变仍然旧路重走的实例也不少。哪怕是带领学生兜圈，也要绕回预设，这样的教学太过机械化。教师教学过程不可避免会有预设外产物。如活动2：其实平移法求面积不再是七年级新有能力，早在小学已经普遍掌握。本课而言，对学生的学情足够了解很关键。活动想表达的仍然是“算着证明”和“说理证明”都是实用的证明方法。对于学生的种种回答，教师应顺势利导，为课所用，也不一定要人人动手操作，灵活处理这些学生已经掌握的知识应用，才是解决之道。

反思2

就课型研究看，新授课的“新”字怎样尽可能的展现，给人感觉不再老腔老调，新意缺失？如何打造生意盎然的智慧课堂？

1、“动”之以“情”

引入学生的活动，载体是创设情境。其实数学情境的创设不需要额外加个设计背景，就可以从最简单的一些数学知识入手，数学的味道更浓，实用价值更高。

2、“晓”之以“礼”

课堂教学尽可能设置学生的活动。以活动为导引，在活动中总结、提炼、提升。在活动中通晓数学原理，数学方法，数学思想，数学“礼貌”（数学的解决问题）。

3、“辩”之以“法”

新知需要检测、反馈，辨析是不可或缺的环节。通过各种形式问题的设定，辨析学习成果的习得率，而辨析检测需要方法。新课的方法习得很关键。

4、“用”之以“道”

新授课总是要将新课所学的方法加以应用。应用的目的又是什么？是“道”，“悟道”。教师教的就是“道”，一节课上要做到道法自然，方能为学生传道。

六、结束语

纵观本课的设计、实践，笔者仍觉得一课一中心的重要性。可能有不少老师会将本课的中心理解偏。就证明这一课，中心无疑是证明的必要性。但是具体落实到每个活动中，教材想表达的意图是什么？每个活动的中心思想是什么？笔者观点是：感受计算证明、操作证明、推理证明的必要性之外，还有一些深意：

1、证明可以为我们提供严谨的说理途径；

2、可以用证明进行严谨的说理；

3、证明的必要性；（为什么要学习证明？）

教材是一本永远读不尽的书，每多读一次，就多一层收获，析透教材，明确主线是数学课的认知前提。捕捉生成，灵动教学是学生学力、能力生长的必须营养。只有与时俱进，不停钻研，才能不断提升教师水平，打造智慧课堂，彰显师生共有智慧。

 

2016年7月8日