《认识几分之一》
教学目标:
1、能结合直观图示初步认识分数,知道分数各部分的名称,能正确地读、写分数。
2、学会比较两个分数的大小,明白平均分的份数越多,每一份就越小。
3、引导学生经历分数创生的过程,培养学生创新意识。
4、体会分数来自生活实际的需要,感受数学与生活的联系,进一步产生对数学的好奇心和兴趣。
教学重、难点:初步认识分数,会比较分数的大小。
教学准备:课件、练习纸
教学过程:
一、初步认识几分之一
1、创设情境,体会分数的含义。
谈话:花果山上住着许多猴子,其中有这样三家。第一家2只小猴,第二家3只小猴,第三家4只小猴。这一天,第1家的猴妈妈下山买了3个同样大的饼,自己家留1个,另外两家各送1个。
(1)引出平均分
师:第一家的猴妈妈该怎样分这个饼才合适呢?
生1:从中间分。
师:这样分成2份?(电脑示错)
师:你的意思是这样来分,每一份要分得同样多。(电脑中间分后对折演示)
师:对,每份分得同样多就是平均分。这样分才公平。(板书:平均分)第一家的猴妈妈把饼平均分成了2份,第2家的猴妈妈把饼怎么分呢?第3家的猴妈妈怎么分?
(2)质疑反问,体会几分之一的含义(几份中的一份)
师:这样每家的每只小猴都吃了其中的一份。同样是一份,一样大吗?
生:不一样大。
师:为什么呢?我们来看,这一份是——(手势引导)这一份是——那这一份呢?
小结:分同样大的一个饼,平均分之后,它是2份中的1份,它是3份中的1份,它是4份中的1份,当然不一样大。
2、激发需要,经历分数的建构过程。
(1)质疑启发:像这样,2份中的1份,3份中的1份,4份中的1份,还能用我们以前学过的1、2、3、4等等来表示吗?那该用什么样的数来表示呢?你能不能想办法创造一个新的数?咱们就以2份中的1份为例,同桌先讨论讨论,试着写一写。
(2)创造分数
(3)交流反馈:(预设有如下几种情况)(指名板演)
① 1/2
② 1/11
③ 2/1
(4)统一写法
师:观察一下,有什么相同的地方吗?同学们写的数中怎么都有数字2和1?这里的2表示什么?1表示?
师:那数学家又是怎么想的呢?(出示图片及录音)
师:现在你们知道选哪一种写法了吧(出示1/2)
3、读、写1/2
(1)读法
师:这个数你会读吗?谁来读读看?
生:二分之一
(2)写法
师:1/2该怎样来写呢?
示范:先用尺画一短横,表示平均分;平均分成了2份,就在横线下面写2,取其中的1份就在横线上面写1。
书空:
师:会写了吗?拿起右手和老师一起再来写一写。先画一条短横线,然后在横线下面写2,最后在横线上写1。
4、回扣1/2的意义
师:这里的1/2表示什么意思?
5、认识、
师:第2家的这一份,用哪个数表示?(出示1/3)表示什么意思?
师:第3家的这一份呢? (出示1/4)表示什么意思?
6、类推、归纳
师:如果把这个饼平均分成6份,其中的一份就是?如果平均分成10份,一份就是?平均分成20份,一份就是?
归纳:看来,平均分之后,几份中的一份就是(几分之一)。
7、揭示课题
(1)师:同学们,刚才认识的1/2、1/3、1/4、(写)1/6等等这些数叫什么数?
生:分数。
(2)师:同学们观察一下,这些分数和我们以前学过的数一样吗?(不一样)哪里不一样?它有几部分组成?中间的一条横线叫做分数线,表示平均分;分数线下面的数叫做分母,表示平均分的份数;分数线上面的数叫做分子,表示取的份数。(板书:分数线 分母 分子)
(3)师:这些分数还有什么特点?
生:分子都是1
师:是的,今天这节课我们一起来重点研究几分之一的分数。(板书课题:认识几分之一)
二、深化认识几分之一。
1、强化单位“1”
(1)求同
师:你能用分数表示涂色部分的大小吗?(出示3个1/5)
师:为什么都能用1/5来表示呢?
生:……
小结:对,只要是平均分成5份,其中的一份都能用1/5表示。
(2)求异质疑
师:那这3个1/5,表示的意思完全一样?有什么不同?(出示“( )的”)
生:五角星的1/5,第2个是巧克力的1/5,第3个是圆的1/5。
师:对,我们还得说清楚是谁的几分之一。
2、强化平均分
(1)出示图
( )的( )/( )
(出示:大三角形 1/2)
(2)出示图
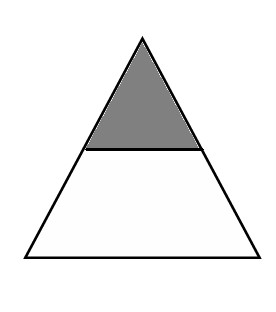
( )的1/( )
师:这个涂色部分也是大三角形的1/2吗?为什么不是?
小结:看来,平均分之后,几份中的一份才能用几分之一表示。
(3)估一估
师:请你估估看,这个涂色部分是大三角形的几分之一?
生估测:1/3、1/4……
师:哦?同学们到底估得对不对呢?一起看大屏幕。(电脑验证)
3、巩固练习
师:接下来,你能很快地表示出每个涂色部分是谁的几分之几吗?请同学们快速完成练习纸上第1题。(5题)
(1)学生独立完成
(2)全班交流反馈
质疑:同学们看,明明涂色部分的形状不同,为什么都能用1/8来表示呢?
小结:看来分法不同没关系。只要是把这个正方形平均分成8份,其中的1份就是它的1/8。
三、比较分数的大小
1、质疑验证,体会分数的大小
(1)猜想质疑
出示分数:1/2○1/4
师:老师这里有两个分数,请你猜猜看,哪个分数大,哪个分数小?
(2)数形结合,验证猜想。
生说理
(3)类化
师:老师这里还有一个分数(出示1/6),跟上面的分数比,谁最小?
生:1/6小。
师:到底对不对呢?我们也拿同样的长方形把它平均分成6份,其中的一份怎样?更小了,所以1/6比这三个分数还要小。
师:如果拿1/10和它们比呢?如果是1/36呢?你发现了什么?把你的发现跟小组同学互相说说。
学生交流
小结:是的,平均分得份数越多,每一份就越小。
2、巩固练习(4组比大小)
过渡:没有图,你还能正确地比出分数的大小吗?
四、全课总结
师:今天我们一起认识了新朋友——分数。通过学习,我们知道把一个图形或物体平均分成几份,一份就是它的(几分之一)。平均分的份数越多,每一份就越(小)。
五、巩固拓展
1、基础练习(填一填)
(1)把一块蛋糕平均分成6份,每份是它的( )/( )。
(2)把一张长方形纸平均分成( )份,每份是它的1/4。
(3)把一根绳子平均分成5段,一段占全长的( )/( );如果把这根绳子平均分成9段,一段占全长的( )/( ),它们的大小是( )>( )
2、生活中的分数
师:同学们,其实在生活中经常可以见到分数。瞧,这是学校的一块黑板,一块是科学天地,一块是艺术园地,你能说出科学天地和艺术园地分别是这块黑板的几分之一吗?
(全班交流,媒体演示)
3、说一说
(1) 涂色部分是大正方形的几分之几?
(2) 涂色部分是大长方形的几分之几?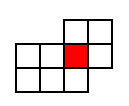
(3) 涂色部分是整个图形的几分之几?
设疑:同样是这个小正方形,为什么用不同的分数表示呢?
师:同样是这个小正方形,比较的标准不同,和正方形比是它的1/4,和长方形比是它的1/6,和整个图形比又是它的1/9。
小结:看来,和不同的标准去比较,表示的分数也就不同。
4、点一点,数轴上认识分数
(1)逐一出示3个长方形,用1、2、3表示;出示半个长方形引导学生用1/2表示
(2)压缩成线段后形成数轴
师:我们把图简化一下变成这样。如果把它看成是一条数轴,那么最左边起始的这个点是用0来表示。后面还有还有很多的数。(电脑演示延长成数轴)
(3)数轴上找1/4
师:0和1之间除了分数1/2,还能找到1/4对应的点吗?谁上来指一指?你是怎么想的?
师:是不是呢?(出示1/4的点)这个点就对应了分数1/4。
师:0和1之间除了1/2、1/4,还有其他的分数吗?(有)
师:是的,0和1之间还有许许多多的分数,它们都能在数轴上都能找到相对应的点,(出示多个点)今后我们会进一步研究学习。
教学反思:
1、创设故事情境,激发学生兴趣。
从整数到分数,对于学生来说是认知上的突破,为了降低孩子跨越难度,我利用创编故事的形式,利用猴妈妈分饼的难题,激发孩子们的学习兴趣。让学生理解一人一半就是每人分得饼的二分之一。我将重点放在认识二分之一上,让学生充分理解了二分之一的含义后,自己创编生活中的二分之一用在哪里,深入理解分数的含义。最后练习设计也按照梯度原则,先易后难,先基础后综合。从学生课上做题情况来看,基础练习做的很好。
2、注重学生的动手实践、自主探索、合作交流。
在教学是,我放手让学生动手操作、自主探索。我提供了多种动手操作的实践机会,让学生通过自己的动手实践和叙述,充分理解“平均分”“二分之一”的含义。接着,让学生把圆形纸片平均分成自己想要的份数,进一步理解几分之一的含义。在教学比较大小时,也是尽量放手,让学生自己去操作、发现。实现了由单一被动式接受向自主探究式学习的转变,培养了学生勇于探索和自主学习的精神,让他们获得了成功体验。
3、合理运用多媒体课件,加强直观教学。
在这节课中,我充分利用课件,让整堂课的教学变得直观,生动有趣,一目了然。降低了认知难度,对学生正确理解几分之一的含义起到了重要作用。例如,在猴妈妈分饼时,充分利用多媒体课件,用动画的方式出现。在理解二分之一的含义时,我在课件上用不同的颜色显示出,让学生直观理解二分之一是把一个饼平均分成两份,每份是它的二分之一。
4、注重学生说的训练。
在整个教学过程中,我随时注意培养学生用数学语言叙述的习惯。比如,在说二分之一的含义时,不但让学生单独说,还让学生小组内交流。让学生通过说,理清自己的思路,找出数学规律,形成数学知识。
附件: